I am currently a Postdoctoral Researcher affiliated with the Norbert Wiener Center for Harmonic Analysis and Applications at the University of Maryland,
under the supervision of Radu Balan
and
Wojciech Czaja.
Before this, I was a postdoctoral fellow affiliated with the Institute for Computational and Experimental Research in Mathematics at Brown University.
I completed my Ph.D. in mathematics in 2022 at the University of California, Davis, under the supervision of
Kevin Luli.
In the broadest terms, my research focuses on making optimal decisions from limited information.
Sample Projects
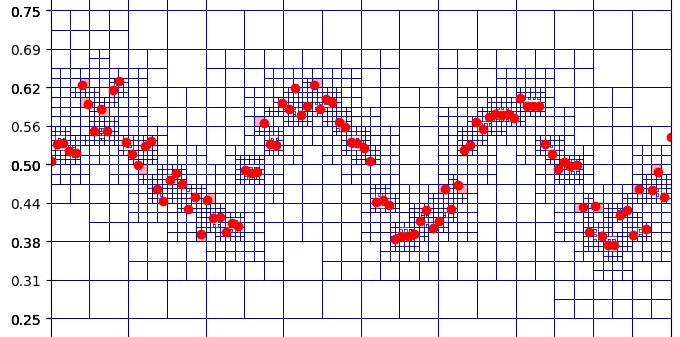
Data Fitting
At the basic level, Whitney's problems ask for efficient and universal ways to fit a function
to random data while minimizing some energies.
Here is an expository article
with an overview of Whitney's problems.
I am particularly interested in how nonlinear constraints,
such as positivity or convexity, preserve or alter the structure of these problems.
The code provides the multiscale decomposition techniques for efficient high-dimensional interpolation algorithms.
Picture: A Whitney decomposition with respect to data sampled near a sine curve.
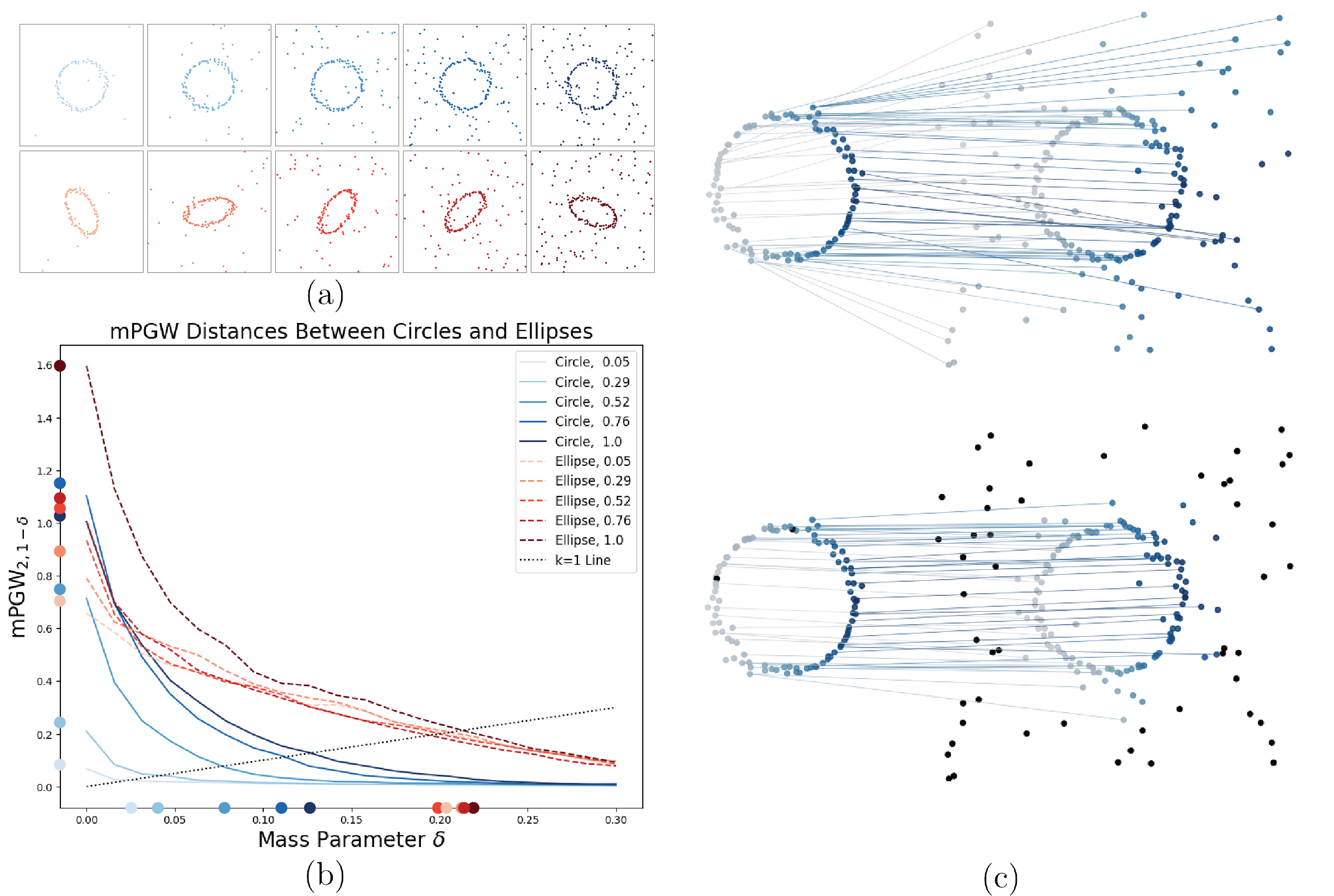
Matching Networks and Pointclouds
The Gromov-Wasserstein (GW) distance is a powerful tool from optimal transport
for comparing datasets across different metric spaces,
widely used in network analysis and geometry processing.
However, GW is sensitive to outliers and cannot handle partial matching.
We study a relaxed version of GW and analyze its geometric properties.
Building on this, we introduce a new family of robust distances that overcome GW's limitations
and offer improved robustness to noise and incomplete data.
Picture: GW distance between two sets of circles and ellipses.
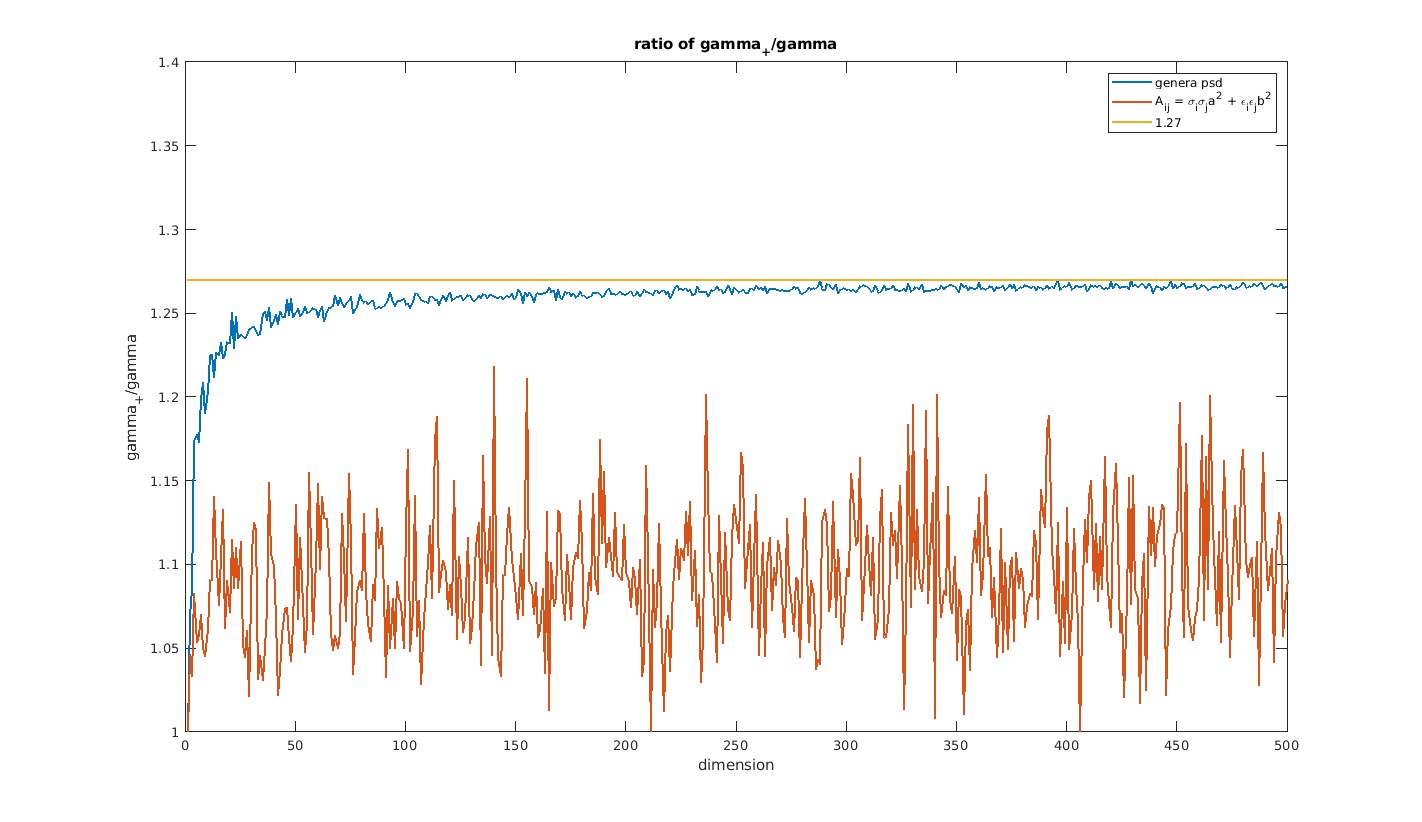
Optimal operator approximation
A problem posed by H. Feichtinger (and subsequently by C. Heil and D. Larson) asks
whether an \(L_1\) version of Mercer's Theorem will hold.
One can formulate the finite-dimensional variant of the problem in terms of optimal matrix factorization in \(\ell_1\).
In a recent preprint with R. Balan,
we showed that the answer is no in general.
Picture: A Monte Carlo simulation of the decomposition.
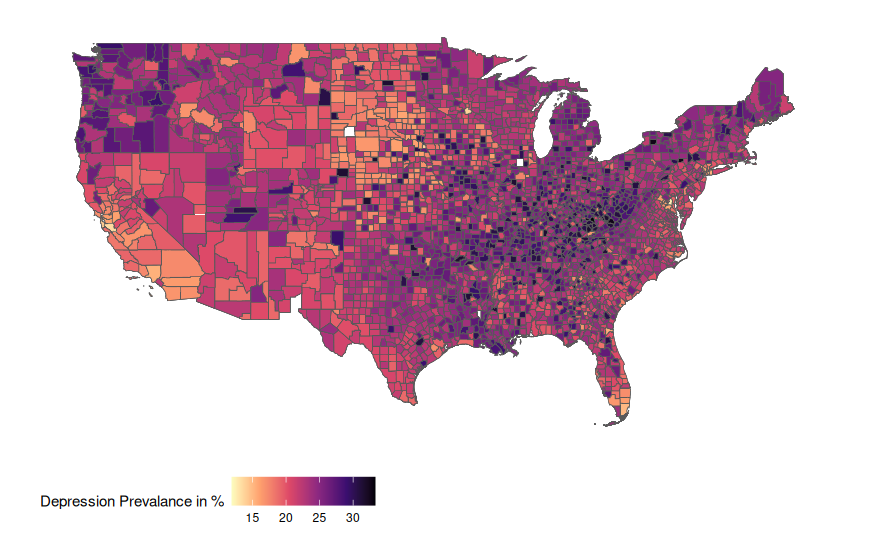
Data Storytelling
An evolving expository including various data visualization projects
that branched off from the Data Visualization course that I taught.
The thumbnail is a map that explores the prevalence of
mental health issue across the US.
